Внешняя неуравновешенность и уравновешивание двигателей

Главный вектор неуравновешенных вращающихся масс, равный геометрической сумме векторов , , и

будет вращаться вместе с коленчатым валом с угловой скоростью ω. При любом положении коленвала проекциями этого вектора на вертикальную и горизонтальную ось будут RrВ и RrГ. Следовательно, численное значение главного вектора неуравновешенных вращающихся масс можно определить из выражения

Если определены проекции главного вектора Rr при положении коленчатого вала, кргда его первый кривошип находится в своей ВМТ, то угол между главным вектором и вертикальной осью φr

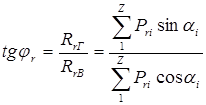
Справедливо и обратное: для произвольного положения коленчатого вала, определяемого углом αi, проекции главного вектора на вертикальную и горизонтальную оси можно найти по уравнениям

RrВ = Rr cos (α1 +φr) RrГ = Rr sin (α1 +φr).

Несколько иначе обстоит дело с неуравновешенными моментами от сил инерции вращающихся масс. Как известно, момент P·a сил , действующих в плоскости ЕЕ, можно представить вектором , перпендикулярным к плоскости ЕЕ. Длина вектора соответствует в выбранном масштабе величине момента. Вектор направлен в ту сторону, откуда пара сил представляется действующей по часовой стрелке. В соответствии с этим вектор момента от силы PriВ направлен горизонтально, а вектор момента от силы PriГ - вертикально.

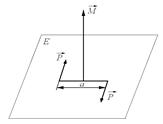
Рис. 8.16 – Вектор изображения момента пары сил

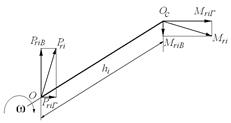
Рис. 8.17 – Схема моментов неуравновешенных вращающихся масс цилиндра

Момент от силы Pri

.

Соответственно

.

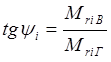Обозначим через ψr угол между результирующим вектором момента Mr и горизонтальной осью. Для главного вектора сил инерции вращающихся масс по аналогии получим

,

;

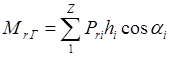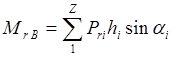
Таким образом

,

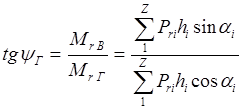откуда непосредственно следует

Mr Г = Мr cos (α1 + ψr);

Mr В = Мr sin (α1 + ψr),

где ψr - начальная фаза момента.

В дальнейшем будем определять ψr для положения коленчатого вала при α1 = 0.

Для сил и моментов сил инерции ПДМ первого и второго порядков получим соответственно:

; ;

; ;

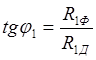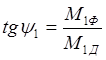R1Д = RI cos (α1 + φ1); M1Д = MI cos (α1 + φ1);

; ;

; ;

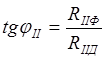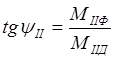R1IД = RII cos (α1 + φ1I); M1IД = MII cos (α1 + φ1I).

Лекция 16. 8.4.2. Определение неуравновешенных сил и моментов от системы сил инерции вращающихся масс

Неуравновешенные силы и моменты принято определять при положении коленчатого вала, когда кривошип первого цилиндра находится в ВМТ.

Рекомендуем также:

Гидрообъемная трансмиссия
Этот вид трансмиссии представляет собой бесступенчатую передачу автомобиля. В гидрообъемной трансмиссии (верхняя половина рис. 6) двигатель 1 внутреннего сгорания приводит в действие гидронасос 2, соединенный трубопроводами с гидромоторами 3, валы которых связаны с ведущими колесами автомобиля. П ...

Проблемы водного транспорта в России
Чтобы внутренний водный транспорт занял достойное место в экономике страны, должны постараться и властные структуры, и судоходное сообщество. С этой целью и была создана Ассоциация судоходных компаний (АСК), объединяющая основных участников судоходного бизнеса на внутреннем водном транспорте. Обще ...

Расчет пропускной способности участков отделения
Максимальные размеры перевозок, которые могут быть осуществлены на ж.д. линии, определяются ее пропускной и провозной способностью. Пропускная способность – это наибольшее число поездов или пар поездов, которое может пропустить ж.д. линия в единицу времени (обычно сутки) при имеющейся технической ...