Динамика кривошипно-шатунного механизма

; (8.5)

. (8.6)

В результате приведённые массы кривошипа примут вид

; , (8.7)

где - масса шатунной шейки;

- масса рамовой шейки.

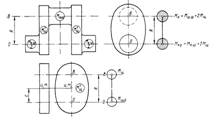
Рис. 8.2 – Кривошип и его динамическая модель

Приведение масс противовеса

Динамическая модель противовеса аналогична модели кривошипа.

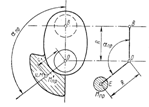
Рис.8.3 – Противовес и его динамическая модель

Приведённая неуравновешенная масса противовеса

, (8.8)

где - фактическая масса противовеса;

c1 – расстояние от центра масс противовеса до оси вращения коленвала;

R – радиус кривошипа.

Приведённая масса противовеса считается расположенной в точке на расстоянии R в сторону центра масс относительно оси коленвала.

Динамическая модель КШМ

Динамическую модель КШМ в целом составляют на основе моделей его звеньев, при этом массы сосредоточенные в одноимённых точках суммируют.

1. Приведённая поступательно-движущаяся масса, сосредоточенная в центре поршневого пальца или поперечины крейцкопфа

MS = MП + МШТ + МКР + МШS, (8.9)

где MП – масса комплекта поршня;

МШТ – масса штока;

МКР – масса крейцкопфа;

МШS – ПДМ части шатуна.

Приведённая неуравновешенная вращающаяся масса, сосредоточенная в центре шатунной шейки

MR = МК + МШR, (8.10)

где MК – неуравновешенная вращающаяся часть массы колена;

МШR – НВМ части шатуна;

Обычно для удобства расчётов абсолютные массы заменяют относительными

; , (8.11)

где Fп – площадь поршня.

Дело в том, что силы инерции суммируются с давлением газов и в случае использования масс в относительной форме получается одинаковая размерность. Кроме того, для однотипных дизелей значения mS и mR изменяются в узких пределах и их значения приводятся в специальной технической литературе.

В случае необходимости учёта сил тяжести деталей, они определяются по формулам

gR = mRg;

gS = mSg,

где g – ускорение свободного падения, g = 9,81 м/с2.

Лекция 13. 8.2. Силы инерции одного цилиндра

При движении КШМ возникают силы инерции от поступательно-движущихся и вращающихся масс КШМ.

Силы инерции ПДМ (отнесённые к FП)

судовой двигатель термодинамический поршневый

qS = -mSJ. (8.12)

Знак "-" потому что направление сил инерции обычно обратно направлено вектору ускорения.

Зная, что , получим

. (8.13)

В ВМТ (α = 0) .

В НМТ (α = 180) .

Обозначим амплитуды сил инерции первого и второго порядков

PI = - mSRω2 и PII = - mSλ Rω2

Получим

qS = PIcosα+ PIIcos2α, (8.14)

где PIcosα – сила инерции первого порядка ПДМ;

PIIcos2α – сила инерции второго порядка ПДМ.

Сила инерции qS приложена к поршневому пальцу и направлена по оси рабочего цилиндра, её величина и знак зависят от α.

Силу инерции первого порядка ПДМ PIcosα можно представить как проекцию на ось цилиндра некоторого вектора , направленного по кривошипу от центра коленвала и действующего так, будто он представляет собой центробежную силу инерции массы mS, расположенной в центре шатунной шейки.

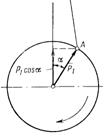
Рис. 8.4 – Векторное изображение сил инерции ПДМ первого порядка

Проекция вектора на горизонтальную ось представляет фиктивную величину PIsinα, так как в действительности такой величины не существует. В соответствии с этим и сам вектор , имеющий сходство с центробежной силой также не существует и поэтому носит название фиктивной силы инерции первого порядка.

Введение в рассмотрение фиктивных сил инерции, имеющих только одну реальную вертикальную проекцию, является условным приемом, позволяющим упростить расчёты ПДМ.

Вектор фиктивной силы инерции первого порядка можно представить как сумму двух составляющих: действительной силы PIcosα, направленной по оси цилиндра и фиктивной силы PIsinα, направленной перпендикулярно к ней.

Рекомендуем также:

Пожарная безопасность
Основными причинами возникновения пожаров на автотранспортных предприятиях являются: неисправность отопительных приборов, электрооборудования и освещения, неправильная их эксплуатация; самовозгорание горючесмазочных и обтирочных материалов при неправильном их хранении; неосторожное обращение с огн ...

Расчет расположения подкладок по длине груза
В соответствии с требованиями ТУ определяем ширину распределения нагрузки на раму платформы и минимальное допускаемое расстояние a между продольной осью подкладки и поперечной плоскостью симметрии платформы. Ширина распределения нагрузки на раму платформы Bн, при размещении на платформе груза на ...

Гидрообъемная трансмиссия
Этот вид трансмиссии представляет собой бесступенчатую передачу автомобиля. В гидрообъемной трансмиссии (верхняя половина рис. 6) двигатель 1 внутреннего сгорания приводит в действие гидронасос 2, соединенный трубопроводами с гидромоторами 3, валы которых связаны с ведущими колесами автомобиля. П ...